検査課の白濱です。
唐突ですが、今日は、フーリエ変換についてお話しします。
これは、私の部下からのリクエストでして、昔の知識を呼び起こしてお話しします。
まず、「フーリエ変換」知らない方は、何の分野の話？となるでしょう。ただ、私が話すことから、数学の分野のお話だとお察しできましたら幸いです。
そんな「面倒な数学の話なんて、御免だ！」と離れていくのは覚悟していますし、まあ、普通に生活していれば、「必要ないじゃん」となりますが、皆様は、数学の恩恵を受けております。
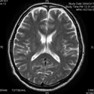
例えば、MRI検査について
MRI検査は、磁石の力を用いて体内から出る信号をとらえて画像を得ます。
出てくる信号は左な感じで、一応、「波形」ですが、 フーリエ変換など画像処理すると右のようになります。
→→→→ 
放射線技師なら、その仕組みに興味がそそられるところですが、私の場合、フーリエ変換の数学的意味の方に興味がそそられます。
ここからは、読者置いてきぼりのフーリエ変換のお話しをしていこうと思います。
それとは別に、分かりやすい数学のお話に興味がある方は、you tubeの「高校数学ひでチャンネル」をお勧めします。（you tubeの検索画面で検索すると、野球の格好をしているアイコンがあります）
さて、世の中の波形は、sin cos の合成で表されて、次のようなフーリエ級数で表されます。
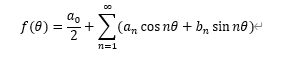
で、フーリエ係数
を求めると、波形を表現できます。ちなみに、フーリエ係数をさらっと書いていますが、ここに至る過程には、「加法定理」や「直交」や「奇関数遇関数」を使っております。これらを、さらに複素数を用い、周期変換を施して、
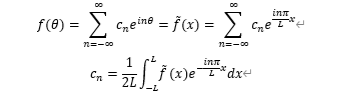
複素形式のフーリエ級数にしたところで、周期を2ｍｌとしｍ→∞ にて整理すると
となり、フーリエ変換は
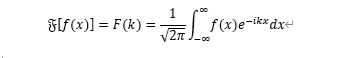
と定義されます。と復習したところで、大学のときに意味も分からず、単位取得のためにひたすら計算していたのは、これだったのか！と20年の時を経て理解しました。最後に、そこに至るまでの過程を書いた直筆のノートの一部を載せて、終わりにします。チャンネル登録お願いします。あっyou tubeじゃなかった！
